Violin Plots: A Powerful Tool for Comparing Group Distributions

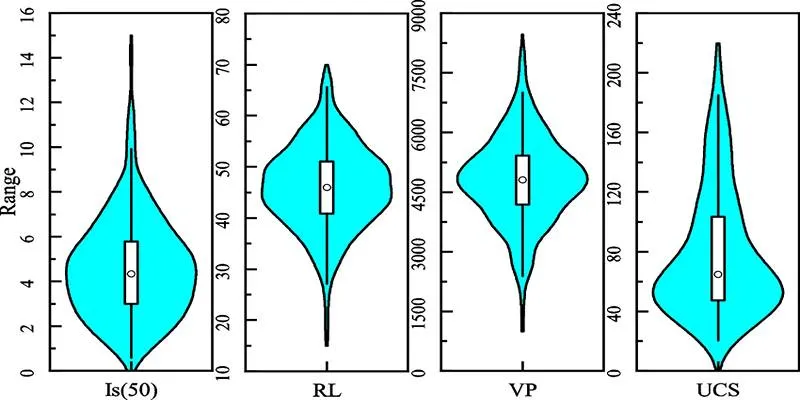
When exploring a dataset, relying solely on summary statistics like the mean or median may not provide a comprehensive understanding. These statistics offer insights into the central tendency of the data but often lack information about its distribution. This is where **violin plots** excel. These plots offer a detailed view of how values are distributed across a variable, merging the simplicity of box plots with the richness of density plots.

This guide delves into **violin plots** as a visual tool for gaining deeper insights into data distribution. Whether you are a beginner aiming to comprehend data variations or an experienced professional fine-tuning model inputs, understanding violin plots is crucial in your data science toolkit.

What Is a Violin Plot?

A violin plot is a hybrid visualization combining features of a box plot and a kernel density plot. It provides a mirrored representation of the probability density of a data distribution around a central axis. In essence, it not only indicates the central tendency and spread of the data but also reveals the shape of the data—highlighting where values are concentrated and where they are sparse.

Unlike box plots, which primarily display quartiles and medians, violin plots present the entire distribution. They enable visual identification of skewness, multimodality (multiple peaks), and outliers with greater clarity.

Main Components of a Violin Plot

Understanding **how to read a violin plot** starts with deciphering the significance of its components:

- **White dot in the center:** Represents the median value of the dataset. - **Thick bar in the middle:** Represents the interquartile range (25th to 75th percentile). - **Thin line:** Extends to the minimum and maximum non-outlier values. - **Violin shape:** Depicts the kernel density estimate. Wider sections indicate higher data density.

The distinctive shape of the violin plot, resembling the body of a violin, is attributed to this density plot component.

Kernel Density Estimation (KDE) in Violin Plots

The violin shape is created using a technique known as **Kernel Density Estimation**. KDE is a method used to estimate the probability density function of a dataset by smoothing out the data to visualize areas of concentration.

Three core aspects of KDE:

• Kernel Function: Assigns weight to each point, often utilizing a Gaussian function.
• Bandwidth: Controls the level of smoothness. Larger bandwidth results in smoother curves, while a smaller bandwidth reveals more detailed features.
• Summation: Combines individual kernels to generate the overall density curve.

In **violin plots**, the KDE is symmetrically mirrored along the axis, giving rise to the characteristic violin shape. This representation provides immediate visual cues regarding the presence of clusters, gaps, or outliers in the data.

When to Use Violin Plots?

Violin plots are particularly beneficial when:

- You need to compare distributions across multiple groups. - You aim to detect patterns, such as bimodal or skewed distributions. - You are analyzing simulation results or residuals in model evaluations.

Due to their ability to combine visual density and statistical summary, violin plots often offer more informative insights compared to box plots alone.

Violin Plot vs. Box Plot vs. Density Plot

Here is a brief comparison of these common tools for visualizing distributions:

Feature	Violin Plot	Box Plot	Density Plot
Shows median	Yes	Yes	No
Displays quartiles	Yes	Yes	No
Detects outliers	Yes	Yes	No
Visualizes density	Yes	No	Yes
Reveals multimodal data	Yes	No	Yes

As evident from the comparison above, **violin plots** offer a comprehensive overview by combining statistical summary and data shape.

Reading Violin Plots: What to Look For

When interpreting a violin plot, consider the following:

- The **width of the plot** at a specific value indicates the proximity of observations to that point. A wider plot signifies more data. - **Symmetry** suggests balanced distributions, while asymmetry hints at skewness. - **Multiple bumps** in the shape imply multiple modes (peaks), indicating subgroups within the data. - **Outliers** are typically represented as small dots outside the main shape, providing insights into rare or extreme values.

Even without numerical labels, a well-designed violin plot offers a powerful visual summary of complex data.

Grouped Violin Plots for Deeper Comparisons

Violin plots are even more impactful when used to compare groups. For instance:

- **Side-by-side violins** facilitate comparisons between different categories. - **Split violins** demonstrate two related distributions (e.g., before and after treatment). - **Colored violins** enhance differentiation across multiple dimensions.

This grouping feature makes violin plots ideal for comparing distributions in segmented data, such as customer categories, experiment groups, or feature groups.

Customizing Violin Plots

Various elements of violin plots can be customized to enhance their informativeness:

- **Orientation:** Horizontal violins can conserve space and enhance readability. - **Points overlay:** Displaying raw data points enhances transparency. - **Bandwidth tuning:** Adjusting KDE bandwidth allows for more or less smoothness. - **Color encoding:** Utilizing different colors for subgroups or categories.

These customization options enable data professionals to tailor violin plots to suit their specific requirements and audience.

Tips for Creating Effective Violin Plots

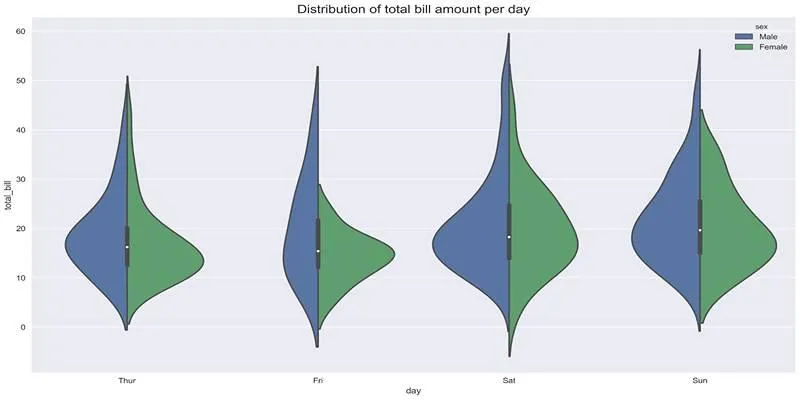
To maximize the utility of your violin plots, approach their design with attention to detail. Violin plots are particularly valuable when dealing with datasets that are **multimodal**, **skewed**, or contain **non-normal distributions**, as they can unveil underlying patterns that may be overlooked by box plots. To enhance their clarity:

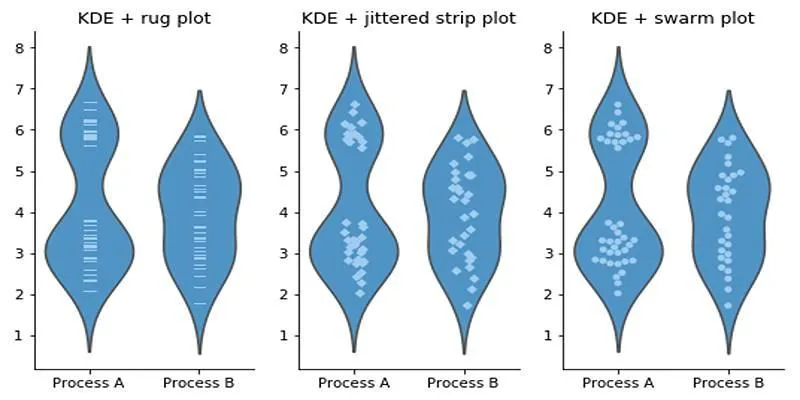
- Consider **overlaying raw data points** (e.g., jittered scatter plots or swarm plots) when dealing with small sample sizes. This provides context and reinforces distribution insights. - If beneficial, **include summary statistics** like the median or quartiles to aid viewers less familiar with violin plots in interpretation. - Carefully select **KDE bandwidth settings**. An excessively large bandwidth may oversmooth the plot, concealing vital structures, while a too-small bandwidth might exaggerate noise. - Be cautious when interpreting the density curve for categories with very few observations, as it may not accurately represent the population.

By adhering to these thoughtful practices, your violin plots can maintain both visual appeal and analytical reliability.

Conclusion

**Violin plots** offer a distinct advantage in data visualization. By amalgamating the statistical insights of box plots with the detailed visualization of density plots, they enable a comprehensive understanding of how data is distributed across categories. Whether analyzing feature distributions or evaluating model outputs, violin plots provide invaluable perspectives.

While they may require some initial acclimatization, **violin plots** help uncover deeper insights hidden within your data. When precision and clarity are paramount, especially in intricate datasets, these plots emerge as an indispensable visualization choice.