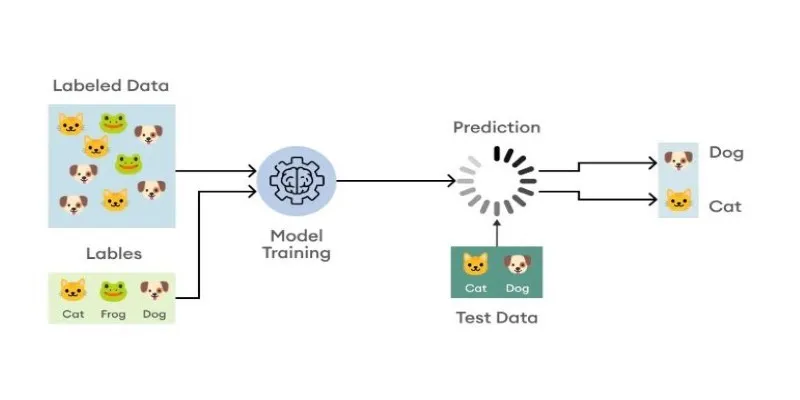
In the world of machine learning, the term “tensor” frequently arises—and for a good reason. Tensors are the fundamental data structures that models use to understand, process, and predict outcomes. While the term might initially seem daunting, with its roots in physics and advanced mathematics, its role in machine learning is highly practical. Tensors are at the heart of everything from image recognition to language translation.
They represent the format data takes as it moves through layers of a neural network. This article aims to simplify the concept of tensors, exploring what they are, how they function, and why they are crucial in real-world machine learning applications. Let’s break it down.
What Exactly Is a Tensor?
A tensor is essentially a structured container for data. It expands upon familiar mathematical objects like scalars, vectors, and matrices. A scalar, a single value, is considered a zero-dimensional tensor. A vector is one- dimensional, while a matrix is two-dimensional. Tensors can be three- dimensional, four-dimensional, or even higher, depending on the data’s complexity. Each additional dimension helps capture more structure. For example, a colored image stored with RGB values can be represented as a 3D tensor with dimensions for height, width, and color channels.
This flexibility is vital in machine learning. Models often require inputs in specific shapes, and tensors provide that precise structure. Natural language processing models might use 3D or 4D tensors to encode sequences of word embeddings across batches. Video models can require even more dimensions to handle time, frame height, width, and channels.
What truly distinguishes tensors is that they are not merely random groupings of numbers—they adhere to mathematical rules. These rules enable fast, parallel computations critical for training models on modern hardware like GPUs and TPUs.
Key Properties That Make Tensors Work
Tensors stand out not only because they are multi-dimensional but also due to their unique properties that make them indispensable in machine learning. The first of these is rank, which refers to the number of dimensions or axes in a tensor. A scalar has a rank of 0, a vector has a rank of 1, and a matrix has a rank of 2. Higher-rank tensors—like those used for image or video data—can have three, four, or even more dimensions. The rank determines how data is structured and interpreted, and models are typically built with very specific expectations for tensor rank.
Another critical property is the shape of a tensor. Shape refers to the size of each dimension and is represented as a tuple. For instance, a shape of (3, 4, 5) means the tensor has three dimensions, with 3, 4, and 5 elements, respectively. Shape affects how tensors are reshaped or split during preprocessing and model operations.
Tensors also have a data type, such as integers, 32-bit floats, or even complex numbers. The type you choose impacts performance and accuracy. Lower- precision data types save memory and speed up training but might reduce result fidelity.
Lastly, tensors support a range of operations—from arithmetic to broadcasting. Broadcasting allows operations on tensors of different shapes by auto- expanding smaller tensors. These properties make tensors fast, adaptable, and ideal for large-scale machine learning computation.
Why Tensors Are So Important in Machine Learning?
Tensors are the beating heart of machine learning. Everything from raw data input to model predictions flows through them. In deep learning models, for instance, input data—whether it’s an image, a text string, or an audio clip—is first transformed into a tensor. This tensor moves through the neural network layer by layer, undergoing various mathematical operations. Weights, biases, activations—all of them are tensors being adjusted during training to improve performance. Without tensors, the entire learning pipeline simply wouldn’t function.
In computer vision, tensors represent images by storing pixel data across dimensions like height, width, and color channels. For natural language processing, individual words or subwords are tokenized into vectors and packed into tensors that can feed into models like BERT or GPT. In reinforcement learning, tensors help define states, actions, and rewards, enabling agents to interact with environments in a structured way.
Tensors are also optimized for scale. When dealing with huge datasets, they make batch operations seamless. Combined with hardware like GPUs and TPUs—built to accelerate tensor computations—the result is faster training and inference times, even on massive models.
Frameworks like TensorFlow, PyTorch, and JAX don’t just use tensors—they’re designed around them. They provide tools to manipulate and compute with tensors, making them the foundation of modern machine-learning systems.
The Role of Tensors in Modern AI Development
Tensors do more than store data—they enable machine learning models to work efficiently and at scale. They serve as the critical link between raw input and the logic of algorithms. No matter the data format—structured spreadsheets or unstructured content like video—tensors allow it all to be fed into models in a consistent and manageable form.

Advances in tensor computation have fueled recent strides in AI. One powerful example is transfer learning, where pre-trained models are adapted for new tasks. This is possible because all the learned knowledge—weights and parameters—is stored in tensors. Fine-tuning a model essentially means modifying its tensors to align with a new goal.
Tensors also drive real-time AI applications, such as object detection in autonomous vehicles or instant voice translation. Their structured format and compatibility with parallel computation enable millisecond-level inference speeds. Optimizations like quantization and pruning rely on tweaking tensor values, reducing size without compromising performance.
Even when debugging, tensors provide insight. A shape mismatch or incorrect data type often causes model errors. Understanding tensors means understanding how your model processes data—and fixing problems when it doesn’t. In every stage of development, tensors are the backbone of modern AI workflows.
Conclusion
Tensors are the lifeblood of modern machine learning. Their power enables data flow, model training, and complex operations across multiple dimensions. Whether you’re working on image recognition, natural language processing, or predictive analytics, tensors are always at work behind the scenes. Their structure, adaptability, and compatibility with high-speed computation make them indispensable. Once you understand how tensors function, you gain deeper insights into how machine learning models truly operate—and that knowledge sets the foundation for building better AI systems.
 zfn9
zfn9