In the expansive realm of algorithmic problem-solving, there are moments when brute-force methods aren’t scalable and greedy techniques fall short. When a solution demands exploring all possibilities within certain constraints, backtracking often comes to the rescue.
Backtracking is a time-tested strategy used to incrementally build solutions and undo choices when a path leads to a dead end. Whether solving puzzles, generating permutations, or navigating mazes, backtracking offers a logical and structured way to handle complex decision trees. This comprehensive guide will explore what backtracking is, how it works, where it’s used, and what challenges and advantages it brings along.
What is Backtracking?
Backtracking is an algorithmic approach used to solve problems step-by- step by building a solution incrementally and reverting or “backtracking” as soon as a certain path is found to be invalid or unfeasible.
Unlike brute-force methods that examine all combinations blindly, backtracking intelligently prunes the search space. It only considers candidates that satisfy the problem’s constraints up to a given point and backtracks immediately when a rule is violated.
In simpler terms, backtracking tries an option, checks if it leads toward a solution, and either continues forward or backtracks to try a different option if it hits a wall.
How Does Backtracking Work?
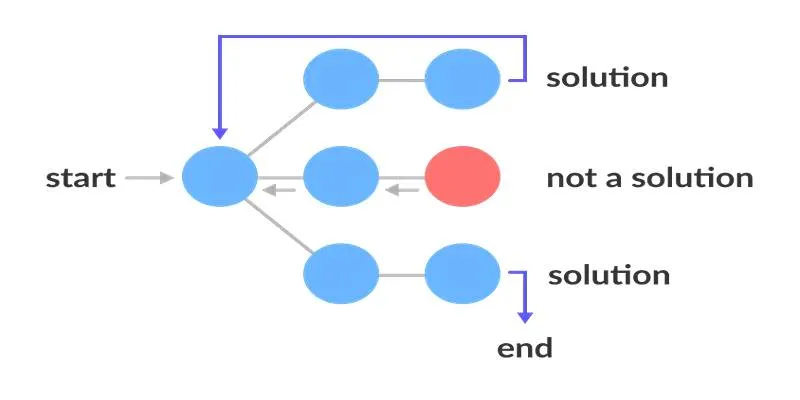
Backtracking operates as a form of depth-first search (DFS). It explores decisions sequentially and backtracks upon encountering constraint violations. Here’s how the process typically unfolds:
1. Recursive Exploration
The algorithm starts at an initial state and makes a decision—such as placing a number or selecting an item. The next decision recursively follows this choice, and so on.
2. Decision Making
At each level, the algorithm picks an option from a set of candidates. These decisions vary by problem: choosing a character in a permutation, assigning a value in Sudoku, or moving in a maze.
3. Constraint Checking
Once a choice is made, the algorithm checks whether it violates any constraints. For instance, in Sudoku, it ensures no repeated numbers in rows, columns, or subgrids.
4. Backtracking
If the decision violates a constraint, the algorithm reverts that choice, returns to the previous state, and tries the next possible option. This prevents the algorithm from wasting time on impossible paths.
5. Solution Validation
If a complete solution satisfying all conditions is found, it is accepted. The algorithm may return one solution, all solutions, or the best solution, depending on the problem.
6. Termination
The process continues until a valid solution is found or all options have been explored, confirming that no solution exists.
When to Use the Backtracking Algorithm
Backtracking may not always be the fastest method, but it’s incredibly versatile for specific problem types, particularly where trial-and-error with constraints is required. Below are common scenarios:
Search Problems with Constraints
Backtracking is ideal when a problem has many possible combinations but only a few valid ones due to constraints. An example is Sudoku, where numbers must be uniquely placed across rows, columns, and subgrids.
Combinatorial Problems
Problems involving combinations and permutations—like arranging objects, placing queens on a chessboard (N-Queens problem), or solving puzzles—are a natural fit for backtracking. It attempts each configuration and prunes those that fail mid-way.
Optimization Problems
In problems like the Knapsack problem, where you must pick items to maximize value without exceeding weight limits, backtracking explores various item selections, discards invalid combinations, and retains optimal ones.
Pathfinding and Maze Solving
Backtracking can navigate paths where multiple routes exist. It tries directions until it hits a wall or dead end, then reverses to try another. It’s perfect for solving mazes or traversing grids with barriers.
Pattern Matching and String Problems
When generating permutations, matching regular expressions, or exploring string combinations, backtracking helps by testing all possibilities and rejecting mismatches.
Game Decision-Making
In strategic games like the 15-puzzle , backtracking explores different moves, retracts those that don’t work, and aims to achieve the goal state through careful trial and error.
Case Study: Sudoku Solving with Backtracking
One of the best real-world illustrations of backtracking is solving a Sudoku puzzle. Here’s how backtracking applies:
-
Find the Next Empty Cell
The algorithm scans the grid to find an empty cell (usually marked as 0). -
Try Possible Numbers (1–9)
For that cell, it tries inserting digits 1 through 9. -
Check for Validity
Before placing a number, it ensures:- The number doesn’t exist in the current row
- The number doesn’t exist in the current column
- The number doesn’t exist in the 3×3 subgrid
-
Place and Recurse
If valid, it places the number and proceeds recursively to solve the rest of the grid. -
Backtrack if Needed
If a placement doesn’t lead to a complete solution, the algorithm removes it (backtracks) and tries the next number. -
Continue Until Solved or Impossible
The algorithm repeats this process until all cells are filled correctly or concludes no solution exists.
This approach guarantees a solution (if one exists) and is a classic example of how backtracking can be used effectively in constraint satisfaction problems.
Applications of Backtracking

Backtracking is widely used in both theoretical and practical scenarios:
- Sudoku Solvers : Ensures numbers are placed according to Sudoku rules.
- Crossword Puzzles : Fills in words in grids while matching intersecting letters.
- N-Queens Problem : Finds valid arrangements where no two queens threaten each other.
- Graph Coloring : Assigns colors to graph vertices such that no adjacent vertices have the same color.
- Task Scheduling : Allocates resources or time slots under constraints.
- Subset Sum Problem : Identifies subsets of numbers that sum to a target value.
- Permutation Generation : Lists all possible arrangements of a set.
- Maze Solving : Finds valid paths from entry to exit.
- Game Tree Exploration : Evaluates moves in strategic games for optimal outcomes.
Conclusion
Backtracking stands as a versatile and logical approach to problem-solving in computer science. It provides a structured way to explore multiple possibilities while systematically discarding the invalid ones.
From puzzles like Sudoku and N-Queens to real-world applications in scheduling and optimization, backtracking has proven its worth in tackling problems that require a methodical exploration of the solution space.
 zfn9
zfn9