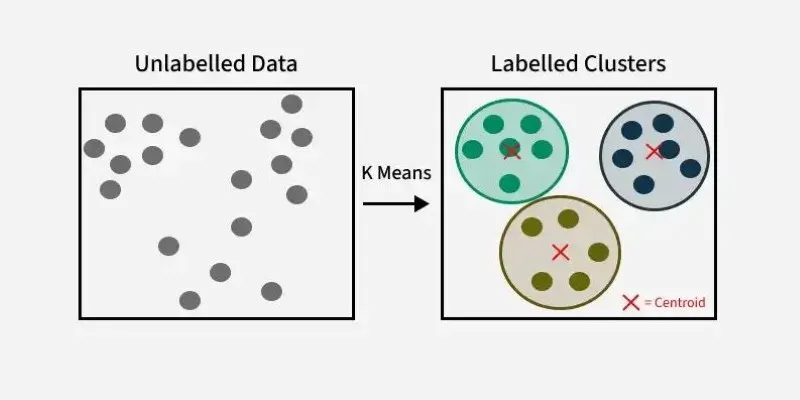
Data is omnipresent, and deciphering it can be daunting. K-Means clustering, a prevalent machine learning algorithm, facilitates this process by grouping similar data points into clusters, thus unveiling hidden patterns. As a pivotal technique in data clustering, K-Means finds applications across diverse fields such as marketing, healthcare, and image recognition, enabling efficient organization of complex datasets. Unlike supervised learning, K-Means requires no labeled data, making it ideal for unsupervised learning scenarios.
Whether it’s segmenting customers, detecting fraud, or simplifying image processing, K-Means plays a crucial role in data-driven decision-making. Understanding its mechanics empowers businesses and researchers to extract meaningful insights from seemingly chaotic information.
How Does K-Means Clustering Work?
K-Means clustering operates through a systematic procedure of dividing data into K groups. The process iterates to improve the clustering of data points. Here’s a step-by-step guide on how it functions:
Choosing K Clusters: The user specifies the number of clusters (K) before running the algorithm. Selecting the right K is crucial as it determines the data partitioning.
Placing Initial Centroids: The algorithm randomly selects K points to serve as the initial cluster centers, known as centroids.
Assigning Data Points: Each data point is assigned to the nearest centroid using a distance metric, typically Euclidean distance.
Recalculating Centroids: Once data points are clustered, the centroids are recalculated to the mean position of all points within a cluster.
Repeating the Process: Steps 3 and 4 are repeated until the centroids stabilize or a predefined number of iterations is reached.
This iterative approach ensures clusters become more refined with each cycle, grouping similar data points into distinct clusters. However, determining the optimal value for K can be challenging.
Choosing the Right Number of Clusters
Determining the optimal number of clusters is a common challenge with K-Means clustering. The elbow method is a popular technique for this purpose. It involves running the algorithm with various K values and plotting the total sum of squared distances between data points and their assigned centroids. The “elbow” point on the chart, where the rate of error reduction slows, typically indicates the ideal K.
Another method is the silhouette score, which evaluates how well each data point fits within its cluster compared to other clusters. A higher silhouette score indicates a better-defined clustering structure.
While these techniques are helpful, real-world applications may necessitate experimenting with different K values to identify the most suitable number for accurate data clustering.
Applications of K-Means Clustering
K-Means clustering boasts numerous applications across various industries due to its ability to efficiently handle large datasets.
Customer Segmentation
Businesses leverage K-Means clustering for market analysis by dividing customers into distinct groups based on purchasing habits, demographics, or online behavior. This enables targeted marketing strategies, personalized recommendations, and enhanced customer experiences.
Image Segmentation and Compression
K-Means clustering is extensively used in image processing, particularly for segmentation and compression. By grouping pixels with similar color properties, the algorithm reduces the number of unique colors in an image, leading to efficient storage and faster processing. This technique is also invaluable in medical imaging, aiding in tumor detection, tissue classification, and anomaly highlighting in X-rays and MRI scans.
Anomaly Detection in Finance and Cybersecurity
In the financial sector, K-Means clustering aids in fraud detection by identifying unusual spending patterns or suspicious transactions. Since fraud often deviates from normal transaction behavior, clustering highlights inconsistencies requiring further investigation. Similarly, in cybersecurity, K-Means detects network anomalies by clustering normal traffic patterns and flagging outliers that may indicate security breaches.
Gene Expression Analysis in Biology
Scientists use K-Means clustering to classify gene expression data, grouping similar gene behaviors. This technique helps identify different cell types, track disease progression, and categorize genetic disorders.
These applications demonstrate how K-Means clustering transcends basic cluster analysis, offering valuable insights that drive innovation across industries.
Strengths and Limitations of K-Means Clustering
K-Means clustering is favored for its efficiency and simplicity, yet it also presents certain limitations.
Advantages
Fast and Scalable: K-Means clustering efficiently handles large datasets, making it ideal for real-time applications.
Easy to Implement: Compared to other machine learning algorithms, K-Means is straightforward and requires minimal computational resources.
Versatile: Its wide range of applications in marketing, healthcare, finance, and image processing makes it a popular choice across industries.
Challenges
Predefined K Value: The need to specify the number of clusters before executing the algorithm can be a limitation, especially when the optimal K is unknown.
Sensitivity to Outliers: Extreme data points can significantly alter cluster centroids, distorting group formations and reducing accuracy, making K-Means clustering sensitive to outliers in real-world datasets.
Assumption of Spherical Clusters: K-Means performs well with spherical, equally-sized clusters. For irregular or overlapping clusters, methods like DBSCAN or hierarchical clustering are more suitable.
Despite these limitations, K-Means remains a fundamental clustering technique. Strategies like K-Means++ initialization can enhance its accuracy by optimizing centroid selection.
Conclusion
K-Means clustering simplifies the complex task of organizing data, making it a foundational machine learning algorithm across various industries. By grouping similar data points, it helps businesses refine marketing strategies, enhance data clustering in image processing, and aid in fraud detection. Its speed and efficiency make it a preferred choice for large datasets, although its sensitivity to outliers and predefined cluster numbers pose challenges. Despite these limitations, K-Means remains a powerful tool for uncovering patterns in raw data. As technology advances, clustering techniques like K-Means will continue to shape data-driven decision-making, offering valuable insights across multiple fields.
 zfn9
zfn9