Probability is a fundamental branch of mathematics that deals with uncertainty, helping to answer questions like, “What are the chances it will rain today?” or “What’s the likelihood of rolling a 6 on a die?” In real-world applications, three essential types of probability are joint probability, marginal probability, and conditional probability.
These three concepts are crucial in fields such as data science, machine learning, healthcare, economics, and weather forecasting. Beyond professional applications, understanding them can help individuals make informed decisions in daily life. This post will guide readers through each type in simple terms, complete with clear examples and comparisons, while maintaining a third-person perspective throughout.
Understanding Joint Probability
Joint probability is the likelihood that two or more events will occur simultaneously. It is typically represented mathematically as P(A and B) or P(A ∩ B), where A and B are events. Joint probability is particularly useful when the outcome depends on two variables or conditions occurring together.
Real-Life Example of Joint Probability
Consider a deck of 52 playing cards. The probability of drawing a card that is both a heart and a queen is a joint probability.
There are 13 hearts and 4 queens in a deck, but only one queen of hearts.
- So, the joint probability of drawing the queen of hearts is:
P(Queen and Heart) = 1/52
In another example, suppose a survey finds that 40 out of 200 people like both pizza and burgers. The joint probability that a randomly chosen person likes both is:
- P(Pizza and Burgers) = 40/200 = 0.2
Characteristics of Joint Probability
-
It indicates the probability of multiple events occurring together.
-
If the events are independent, their probabilities are multiplied. For example:
P(A and B) = P(A) × P(B) -
It is used in situations where combinations of outcomes are relevant.
Understanding Marginal Probability
The marginal probability of an event is the likelihood that it will occur regardless of the outcome of another event. This type of probability is often derived from total or “marginal” values in a data table, hence the name.
Simple Example of Marginal Probability
Suppose a classroom has 30 students:
- 18 are girls
- 12 are boys
The marginal probability of selecting a girl at random is:
- P(Girl) = 18/30 = 0.6
This calculation is done without considering any other characteristics, such as whether students wear glasses or play sports.
Characteristics of Marginal Probability
- It involves a single event or variable.
- It is calculated by dividing the number of favorable outcomes by the total number of outcomes.
- It is called “marginal” because it often appears in the margin (totals) of frequency tables.
Understanding Conditional Probability
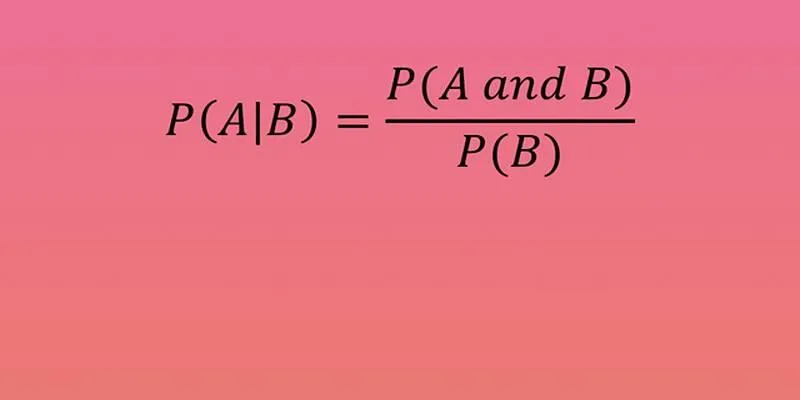
Conditional probability is the likelihood that an event will occur given that another event has already occurred. It is symbolized as P(A | B), which reads as “the probability of A given B.” This concept is crucial when dealing with dependent events, where the outcome of one event affects the outcome of another.
Example of Conditional Probability
Suppose 100 students took a math test. Out of those:
- 60 were girls
- 40 of the girls passed the test
The conditional probability that a student passed the test given they are a girl is:
- P(Passed | Girl) = 40/60 = 0.67
This means that among girls, there’s a 67% chance a randomly selected one passed.
The Formula for Conditional Probability
To compute conditional probability :
P(A | B) = P(A and B) / P(B)
This formula helps isolate a specific subset (like only the girls in the example) to compute more focused probabilities.
How the Three Types Relate
Though these probabilities differ in definition, they are deeply connected.
Consider the formula for conditional probability again:
P(A | B) = P(A and B) / P(B)
This equation shows that conditional probability uses both joint and marginal probabilities. Specifically:
- The numerator is the joint probability (both A and B happen).
- The denominator is the marginal probability (just B happens).
Comparing the Three: A Table Summary
| Probability Type | Focus | Formula | Use Case Example |
|---|---|---|---|
| Joint Probability | A and B both happen | P(A and B) | Rolling a 3 and getting a head on a coin |
| Marginal Probability | A happens, ignore others | P(A) | Chance of a person liking pizza |
| Conditional Probability | A happens, given B already happened | P(A | B) = P(A and B)/P(B) |
Application in Real Life
Understanding these three types of probabilities is crucial in various industries. Below are some examples:
In Healthcare
- Joint probability: A patient has both diabetes and high blood pressure.
- Marginal probability: The overall percentage of patients with diabetes.
- Conditional probability: A patient has diabetes, given they are overweight.
In Marketing
- Joint: A customer clicks an ad and makes a purchase.
- Marginal: The total percentage of customers who visit a website.
- Conditional: Purchase rate given the customer clicked an ad.
In Sports Analytics
- Joint: A player scores and assists in the same game.
- Marginal: A player’s goal-scoring rate across all games.
- Conditional: The chance of a goal given the player is in the penalty box.
Common Misunderstandings
Many people confuse these probabilities, especially conditional and joint. Here’s how to clarify:
- Don’t assume dependence : Joint probability doesn’t always mean events affect each other.
- Watch for overlapping terms : “And” signifies joint; “Given” indicates conditional.
- Use the right total : For marginal probability, always divide by the overall total, not just a subset.
Conclusion
In conclusion, joint, marginal, and conditional probability are key concepts that help explain how likely events are to occur—whether alone, together, or based on other events. Joint probability shows the chance of two things happening at once. Marginal focuses on just one event, and conditional looks at outcomes based on known conditions. These ideas are used in many areas like healthcare, business, and technology. Understanding the differences helps make smarter predictions and decisions. With practice, even beginners can use them confidently. Mastering these basics builds a strong foundation for deeper learning in statistics and data analysis.
 zfn9
zfn9