Mastering Local Search Algorithms in AI for Smarter Optimization

When solving complex problems in artificial intelligence, efficiency matters. Imagine you’re tasked with planning delivery routes, scheduling machines in a factory, or designing a neural network. You need a solution—fast. This is where local search algorithms come in.

Local search is an optimization technique used in AI to explore solutions within a specific neighborhood. It doesn’t attempt to evaluate every possibility like exhaustive search. Instead, it focuses on improving one solution step-by-step by evaluating nearby alternatives. It’s simple, intuitive, and often surprisingly powerful. But it’s not flawless.

In this guide, you’ll explore how local search algorithms work, their common variations, real-world applications, and strategies to overcome their limitations. Whether you’re building AI systems or solving practical business problems, these techniques can take your solutions from average to exceptional.

Fundamental Process of Local Search Algorithms

Local search follows a structured sequence of actions:

1. Initialization: Choose a starting solution, either randomly or based on a heuristic.
2. Evaluation: Calculate the objective or cost function for the current solution.
3. Neighborhood Generation: Identify small changes or perturbations to form nearby solutions.
4. Selection Criteria: Evaluate neighboring solutions and select the best (or acceptable) one.
5. Update: Move to the selected neighbor if it meets the improvement criteria.
6. Termination: Stop when a certain number of iterations is reached, or no better solution can be found.

This process continues iteratively, refining the solution with each step.

Common Types of Local Search Algorithms

Several algorithms fall under the local search umbrella, each with unique strengths and trade-offs:

1. Hill Climbing

This is the most straightforward method. It chooses the neighboring solution that offers the highest improvement and continues until no further gains can be made. However, it often gets stuck in local optima.

Variants include:

• Steepest-Ascent Hill Climbing: Checks all neighbors before choosing the best.
• Stochastic Hill Climbing: Picks a random neighbor and accepts it if it improves the result.
• Random Restart Hill Climbing: Repeats the process from different starting points to avoid local traps.

2. Simulated Annealing

Inspired by the metallurgical process of annealing, this algorithm allows occasional “bad” moves to escape local optima. Over time, the probability of accepting worse solutions decreases, guiding the system toward a global optimum.

Key idea: At high “temperature,” the algorithm explores freely. As it cools, it becomes more selective.

3. Tabu Search

This method remembers previously visited solutions using a “tabu list” to avoid going in circles. It’s effective in exploring more diverse areas of the solution space without repeating mistakes.

It balances exploration (searching new areas) with exploitation (focusing on promising directions).

4. Genetic Algorithms (GA)

Though typically grouped with evolutionary algorithms, GA employs local search concepts like mutation and crossover to evolve better solutions across generations. It works with a population of solutions instead of just one.

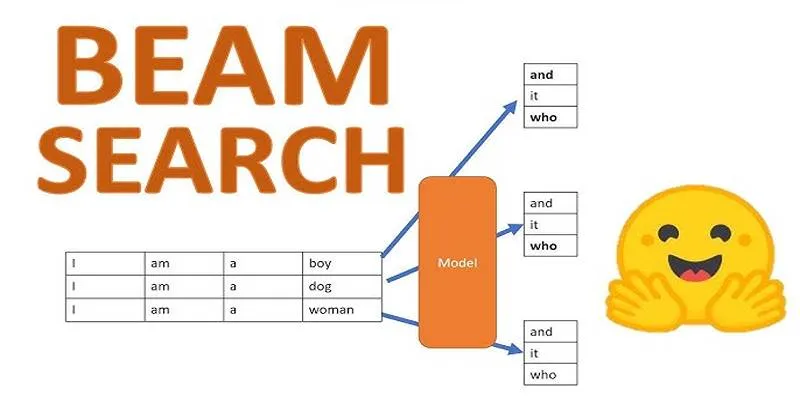
5. Local Beam Search

This algorithm maintains multiple solutions at each step and only keeps the top-performing ones. It reduces the risk of getting stuck by widening the search space compared to single-solution methods.

When and Why Local Search Fails?

Local search algorithms are simple, but not foolproof. Here’s where they commonly fall short:

• Stuck in Local Optima: Without escape mechanisms, algorithms like hill climbing halt at the nearest peak, missing better global solutions.
• Plateaus: In flat search areas where neighbors yield similar scores, algorithms may struggle to progress.
• Poor Initial Solution: Starting too far from optimal regions can waste resources or misguide the search.
• Inflexible Parameters: Poorly tuned step sizes, temperature schedules, or tabu tenure can reduce effectiveness.

Advanced Enhancements to Boost Performance

To address these challenges, several enhancements have been developed:

• Multiple Restarts: By starting the algorithm from various initial points, you increase the chances of finding better solutions and avoid getting stuck in suboptimal regions.
• Hybrid Algorithms: Combining two or more search techniques (e.g., simulated annealing followed by hill climbing) can balance exploration and exploitation more effectively.
• Dynamic Neighborhood Scaling: Instead of using fixed-size neighborhoods, adaptive scaling allows the search to broaden or narrow the search region based on current performance.
• Parallel Search Execution: Running multiple search processes simultaneously increases efficiency and improves the likelihood of identifying optimal solutions.

These tactics help your local search adapt and improve in more complex or noisy environments.

Tips for Implementation Without Code

You don’t need exact code snippets to use local search. Here’s a generalized implementation guide:

1. Define the Objective: Write down what you want to minimize or maximize.
2. Create a Representation: Think of how to express a potential solution—like a list, a graph path, or a configuration.
3. Generate Neighbors: Decide how you’ll tweak your solution—swap elements, change values, or adjust structure.
4. Evaluate Each Neighbor: Score them using your objective function.
5. Choose the Best One: Replace the current solution if the neighbor is better (or acceptable under your rules).
6. Repeat Until Done: Stop if the solution doesn’t improve, if the maximum number of steps is reached, or if results stabilize.

No matter your language or platform, these steps apply to any local search scenario.

Metrics for Evaluating Local Search Performance

To determine whether a local search algorithm is effective, it helps to define measurable metrics:

• Convergence Speed: How quickly does the algorithm find a stable solution?
• Solution Quality: Is the final solution close to the global optimum?
• Iteration Efficiency: How many iterations are needed before improvements stop?
• Robustness: How consistent are results across multiple runs?

Using these metrics allows for a systematic comparison between different algorithms or configurations.

Conclusion

Local search algorithms offer a practical, flexible, and often powerful approach to optimization in artificial intelligence. From scheduling and logistics to robotics and design, these techniques shine in problems where exhaustive search isn’t feasible.

That said, they’re not silver bullets. To make the most of them, choose the right algorithm, tune parameters carefully, and remain mindful of their limitations. And when things get stuck, don’t be afraid to mix and match techniques to break through.

By mastering local search, you’re not just solving AI problems—you’re learning how to tackle complexity itself, one step at a time.