Machine learning thrives on patterns found in probability distributions. But how can we measure how close a model’s predictions are to reality? That’s where KL Divergence , or Kullback-Leibler Divergence , comes into play. Rooted in information theory, it’s more than a formula—it’s a way to measure how one distribution strays from another. It helps models recognize uncertainty, adjust predictions, and refine learning.
KL Divergence acts like a compass for optimization, influencing everything from neural networks to generative AI. Quietly, it has become a foundational tool in modern machine learning. This article breaks down its meaning, function, and lasting impact.
Understanding KL Divergence: The Heart of Distribution Comparison
At its core, KL Divergence is a measure of how one probability distribution diverges from a second reference distribution. Think of it like this: suppose you believe the weather forecast predicts a 70% chance of rain tomorrow. But the actual weather pattern says there’s only a 40% chance. The difference between what you expected (your model) and reality (true distribution) creates an informational “gap.” KL Divergence quantifies that gap.
Mathematically, KL Divergence is defined for two distributions, P (true distribution) and Q (predicted distribution):
KL(P || Q) = Σ P(x) * log(P(x)/Q(x))
This equation tells us how inefficient it is to use Q to approximate P. It’s
not symmetric, meaning KL(P || Q) ≠ KL(Q || P). That’s important because KL
Divergence isn’t just measuring “distance” like Euclidean metrics—it’s about
information loss. When a machine learning model tries to approximate a real
distribution using a learned distribution, KL Divergence acts like a warning
signal that says: “You’re off—here’s by how much.”
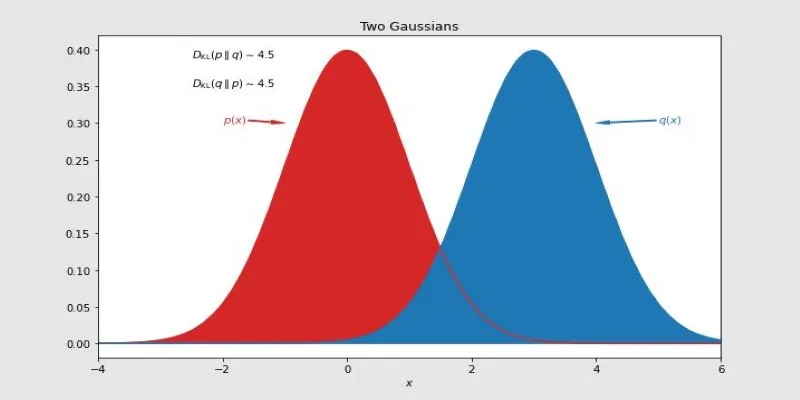
It’s also worth noting that KL Divergence always yields a non-negative value. The lower the value, the closer the two distributions are. A KL Divergence of zero means perfect overlap—the predicted distribution matches the true one completely.
The Role of KL Divergence in Machine Learning Models
KL Divergence holds a central place in modern machine learning, especially in models that operate on probability distributions. One of its most notable roles is in Variational Inference , where it helps approximate complex posterior distributions that are otherwise difficult to compute. This technique underpins Variational Autoencoders (VAEs) —a popular generative model that learns compact representations of input data.
In a VAE, the encoder maps input data to a latent space while the decoder reconstructs it back. However, instead of allowing the latent space to freely adjust, the model uses a KL Divergence term as a penalty. This penalty encourages the latent distribution to stay close to a simpler prior distribution—usually a standard normal distribution. This prevents overfitting and promotes better generalization across new data.
KL Divergence is also fundamental in regularization for probabilistic models. In tasks like language modeling or classification, models often predict probability distributions over words or labels. Minimizing the KL Divergence between these predictions and the true distributions sharpens model accuracy and consistency.
In reinforcement learning, KL Divergence plays a stabilizing role. Algorithms such as Proximal Policy Optimization (PPO) use it to limit the deviation between updated policies and their previous versions, preventing overly aggressive changes that can destabilize learning.
Finally, in Bayesian machine learning, KL Divergence measures how closely an approximate posterior matches the true posterior. This is especially useful in uncertainty-aware systems, where decisions must consider confidence levels, not just outcomes. Whether it’s for compression, regularization, or stability, KL Divergence remains a vital mechanism guiding models to learn smarter, more reliably, and with greater awareness of their limitations.
Why KL Divergence Outshines Other Metrics?
There are many ways to measure differences between distributions, but KL Divergence brings something unique to the table. Unlike mean squared error (MSE) or L1 loss, which measures simple numeric differences, KL Divergence understands the structure of uncertainty. It treats every data point as a piece of a larger probabilistic story and penalizes models based on how they reshape that story.
This makes it especially powerful for applications where precision in probability is crucial. Consider language modeling. Predicting the correct next word isn’t just about picking the top word—it’s about distributing probability across likely words in a way that mimics natural language. KL Divergence penalizes models that assign a high probability to unlikely words and rewards those that align with actual language patterns.
Another strength of KL Divergence is its use in information gain. It answers a fundamental question: “How much extra information do I need if I use distribution Q instead of the true distribution P?” That’s why it’s useful not just in model evaluation but also in guiding model improvement.
However, it’s not without limitations. Because KL Divergence is asymmetric, using it blindly can lead to confusing results depending on which distribution you treat as the reference. It also becomes unstable when Q assigns zero probability to outcomes that P considers likely—this leads to infinite divergence. That’s why smoothed or modified versions of KL Divergence are often used in practice.
Despite this, its impact is unmistakable. As machine learning moves toward more probabilistic and uncertainty-aware models, the ability to fine-tune and guide training through metrics like KL Divergence becomes not just useful but necessary.
Conclusion
KL Divergence isn’t just a mathematical formula—it’s a guiding principle in the world of machine learning. Quantifying how one distribution diverges from another gives models a way to measure their understanding of the data and make corrections when they stray off course. Whether it’s powering deep generative models, helping policies evolve in reinforcement learning, or refining probabilistic inferences, KL Divergence is at the core of many AI breakthroughs. Its ability to translate uncertainty into actionable insight makes it indispensable. As machine learning continues to evolve, the role of KL Divergence will only become more central and impactful.
 zfn9
zfn9