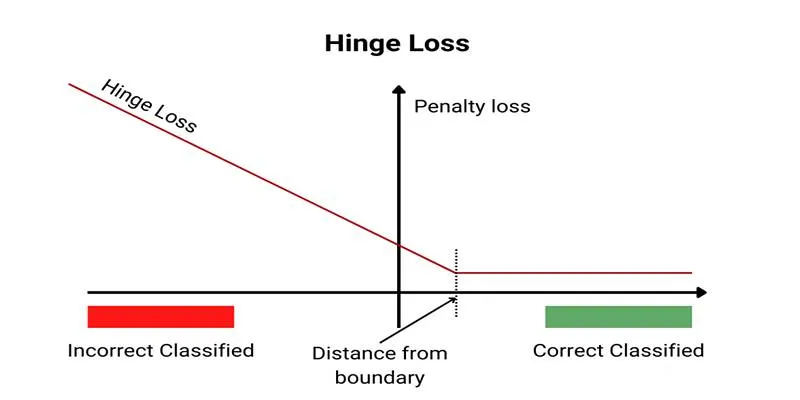
Building a reliable machine learning model isn’t just about feeding it data—it’s about ensuring it truly learns. A model might perform well during training but fail miserably when faced with new information. This failure often occurs when the model memorizes patterns instead of understanding them. Cross-validation is a powerful technique to prevent this issue.
Cross-validation involves several data splits to verify that the model can handle real-world applications. Without it, predictions can be misleading, and overfitting becomes a significant problem. It’s not merely a step in model training but a safeguard against models that appear perfect on paper but can’t deliver in practice.
The Purpose of Cross-Validation
When creating a machine learning model, it is crucial that it performs well on data outside the training dataset. If not tested, the model may excel during training but falter when exposed to new data. This occurs because the model could memorize training patterns rather than truly learning them.
Cross-validation acts as a checkpoint. It systematically divides the data into multiple training and testing sets to assess how well the model generalizes. By repeating this process across various splits, we obtain a more accurate performance estimate. The most common type, k-fold cross-validation, partitions the dataset into k equal-sized parts and uses each part as a test set while training on the other k-1 parts. This is repeated k times, and the outcome is averaged to obtain a final performance measure.
One major advantage of cross-validation is its utility in hyperparameter tuning. Many machine learning models have parameters, known as hyperparameters, that influence their behavior. Rather than guessing optimal settings, cross-validation enables us to try various configurations and choose the one that performs well across different data splits.
Different Types of Cross-Validation
Cross-validation comes in several forms, each suited to various types of datasets and problems. Although k-fold cross-validation is most commonly used, other methods offer specialized benefits based on different circumstances.
K-Fold Cross-Validation
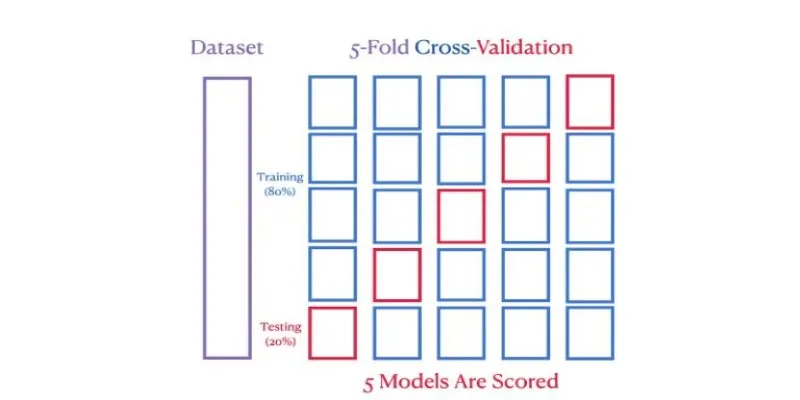
This is the most popular technique, where the dataset is divided into k subsets or “folds.” The model is trained on k-1 folds while the remaining fold is used for testing. This process repeats k times, ensuring that every fold is used as a test set once. The final accuracy is calculated as the average of all k runs. A common choice for k is 5 or 10, but it can be adjusted based on the dataset size.
Stratified K-Fold Cross-Validation
Stratified k-fold cross-validation improves upon k-fold by ensuring each fold maintains the same class distribution as the original dataset. This is crucial for imbalanced data, where a standard k-fold split might create folds with too few minority class samples, leading to unreliable results. By preserving class proportions, stratified k-fold provides a more accurate model evaluation.
Leave-One-Out Cross-Validation (LOOCV)
As the name suggests, this method trains the model on the entire dataset except for one instance, which is used for testing. This process repeats for every data point in the dataset. While LOOCV provides an extremely thorough evaluation, it can be computationally expensive for large datasets, as it requires training the model multiple times.
Leave-P-Out Cross-Validation
This is an extension of LOOCV where, instead of leaving out just one data point, p data points are excluded in each iteration. This provides more flexibility but is even more computationally demanding as the number of possible training-test combinations grows significantly with larger datasets.
Time Series Cross-Validation
Standard cross-validation isn’t suitable for time-dependent data like stock trends or weather forecasts. Time series cross-validation trains on past data and tests on future data, preserving the natural order. This prevents unrealistic evaluations where a model learns from future data that wouldn’t have been available during real-time predictions, ensuring a more accurate assessment.
Benefits and Challenges of Cross-Validation
Cross-validation provides a more reliable estimate of a model’s performance on unseen data. Unlike a single train-test split, it ensures each data point is used for both training and testing, reducing bias and improving model reliability. Evaluating performance across multiple splits helps prevent overfitting, ensuring models generalize well to real-world data. Additionally, cross-validation is useful for selecting the best model among multiple candidates, as it identifies the most consistent and accurate option.

However, cross-validation has its challenges. The most significant is the computational cost, as running multiple training and testing cycles can be resource-intensive, especially for large datasets and deep learning models. This makes it impractical in some cases where computational power is limited. Another issue is data leakage, which occurs if information from the test set influences training, leading to overly optimistic performance estimates. This often happens when data preprocessing, such as normalization or feature selection, is done before splitting the data. To ensure accurate results, cross-validation must be implemented carefully, maintaining a strict separation between the training and testing stages.
When to Use Cross-Validation
Cross-validation is not always necessary, but it is crucial in cases where limited data is available. If a dataset is small, a single train-test split might not provide enough information to evaluate the model accurately. In such cases, cross-validation maximizes the use of available data by ensuring multiple evaluations.
It is also essential when testing multiple models or tuning hyperparameters. Since different configurations may perform differently depending on how data is split, cross-validation helps identify the most stable approach.
However, for extremely large datasets, a simple train-test split may be sufficient. When millions of data points are available, dividing a portion for validation provides a reasonable estimate of model performance without the added computational burden of cross-validation.
Conclusion
Cross-validation is a crucial technique in machine learning that ensures models generalize well to unseen data. Systematic splitting of data into training and testing sets prevents overfitting and provides a reliable performance estimate. Different methods, such as k-fold and stratified cross-validation, cater to various needs. While computationally intensive, its benefits outweigh the challenges, especially for small datasets. Proper implementation leads to more trustworthy predictions, making cross-validation an essential step in building robust and effective machine-learning models.
 zfn9
zfn9